写在前面
本文主要参考了 Pecco的知乎专栏,并在线段树概念介面增加了更多笔墨和证明,期望能给后续自身复习和他人学习带来更多帮助。由于个人疏于 C++ 语言,因此重新使用 Java 语言进行了实现。
线段树介绍
线段树(Segment Tree)是一种主要用于维护区间信息(要求满足结合律)的数据结构,它支持 $O(logn) $复杂度的区间修改和 $O(logn)$ 复杂度的区间查询。
线段树的每个节点都对应一条线段(区间)的某种运算结果(通常是乘积或加和,下面均以加和为例),其中根节点对应整个区间的和。对于某个非叶子节点 $node[left, right]$,其左右子节点对应区间可表示如下:
- $node.left[left, mid]$
- $node.right[mid + 1, right]$
- $mid = \lfloor{(left + right) / 2)}\rfloor{} \ or \ \lfloor{(left + right + 1) / 2}\rfloor{} - 1$
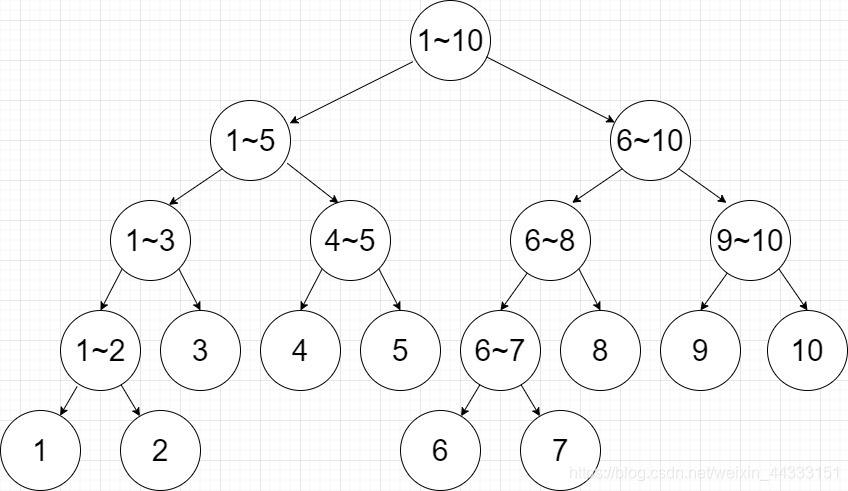
为了更加直观,这里以区间 $[1, 5]$ 为例,对两种不同划分情况建立的线段树进行可视化:
可以看出线段树所有节点的左右子树高度差至多为1,因此线段树是一颗平衡二叉树。
接下来我们探讨线段树的存储方式。通常我们会将线段树存储在数组里,那么对于长度为 $n$ 的原数组,存储它的数组的大小应当为多少?
答案是至少为 $2n - 1$,至多为 $4n - 5$。让我们来简单证明下。
对于一颗线段树,其叶子节点的数量为 $n$,因此其非叶子节点的数量为 $n - 1$,你可以很容易证明它,因为线段树的非叶子节点要么没有子节点,要么左右节点都不为空。所以存储线段树的数组大小至少为 $2n - 1$。
$$
n_0 + n_1 + n_2 = 2n_2 + n_1 + 1 -> n_2 = n_0 - 1 = n - 1
$$
但考虑如方式二种所示情况,因为使用数组存储,所以最后一层中为空的节点同样需要消耗数组空间。此时线段树的倒数第二层的节点数量为 $n - 2 + 1 = n - 1$,因此最后一层为空的节点数为 $2(n - 1) - 2 = 2n - 4$,所以整个数组的大小为 $2n - 4 + 2n - 1 = 4n - 5$。
而容易得知方式二就是最快的情况,所以一般建立线段树数组时需要开辟 $4n$ 的存储空间。
线段树的建立
那么如何从数组中建立一棵线段树?我们可以考虑递归地进行。假设输入数组为 $nums$, 长度为 $n$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
int[] tree = new int[4 * n];
// left, right为输入数组的左右区间点,p为待建立线段树的节点下标
public void build(int left, int right, int p){
// 叶子节点
if(left == right){
tree[p] = nums[left];
}else{
int mid = left + (right - left >> 1);
// 先建立左右节点
build(left, mid, p * 2 + 1);
build(mid + 1, right, p * 2 + 2);
// 该节点的和等于左右节点的和
tree[p] = tree[p * 2 + 1] + tree[p * 2 + 2];
}
}
|
这里是一张来自网上的 $gif$ 图,它描述了对 $[1,2,3,4,5]$ 建立线段树的过程:

线段树的修改
仿照线段树的建立,我们也可以采用递归的方式进行修改,但这样的时间复杂度会比较高。而通常则会引入懒标记来加速这一过程,这也是线段树的精髓所在。使用懒标记后,对于恰好是线段树非叶子节点的那些区间,我们不再递归下去,而是打上一个标记,等到将来要用到它的子区间时,再向下传递。假设需要修改的区间为$[left, right]$,修改的量为 $d$,那么修改过程可以表示为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
int[] mark = new int[4 * n];
public void update(int left, int right, int d){
update(left, right, d, 0, 0, n - 1);
}
// cLeft, cRight代表当前要修改的线段树区间
public void update(int left, int right, int d, int p, int cLeft, int cRight){
// 修改区间不包含线段树区间
if(left > cRight || right < cLeft){
return;
}else if(cLeft >= left && right >= cRight){ // 修改区间完全覆盖线段树区间
tree[p] += (cRight - cLeft + 1) * d; // 直接修改对应区间值
if(cLeft != cRight){ // 并给非叶子节点打上标记
mark[p] += d;
}
}else{ // 修改区间与线段树区间存在重叠,则二分递归地修改
int mid = cLeft + (cRight - cLeft >> 1);
mark[p * 2 + 1] += mark[p]; // 将当前节点的标记分发给其子节点
mark[p * 2 + 2] += mark[p];
tree[p * 2 + 1] += mark[p] * (mid - cLeft + 1); // 子节点的值叠加父节点的标记量
tree[p * 2 + 2] += mark[p] * (cRight - mid);
mark[p] = 0; // 因为已经把懒标记给了子节点,所以本身的标记置0
}
}
|
有同学可能会疑惑这个更新操作在修改区间完全覆盖线段树区间时没有更新整个线段树,但其实我们后续查询的过程中也会根据懒标记对节点值更新,所以不必担忧。
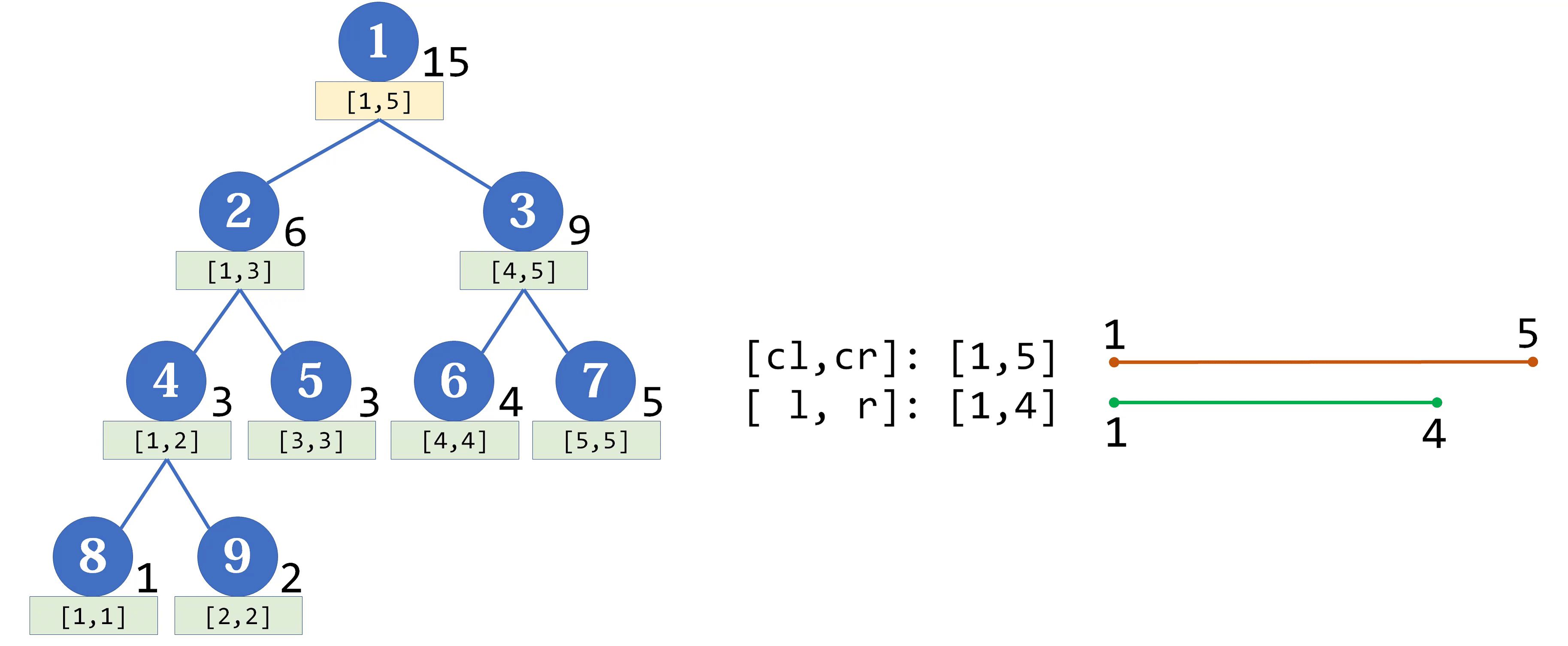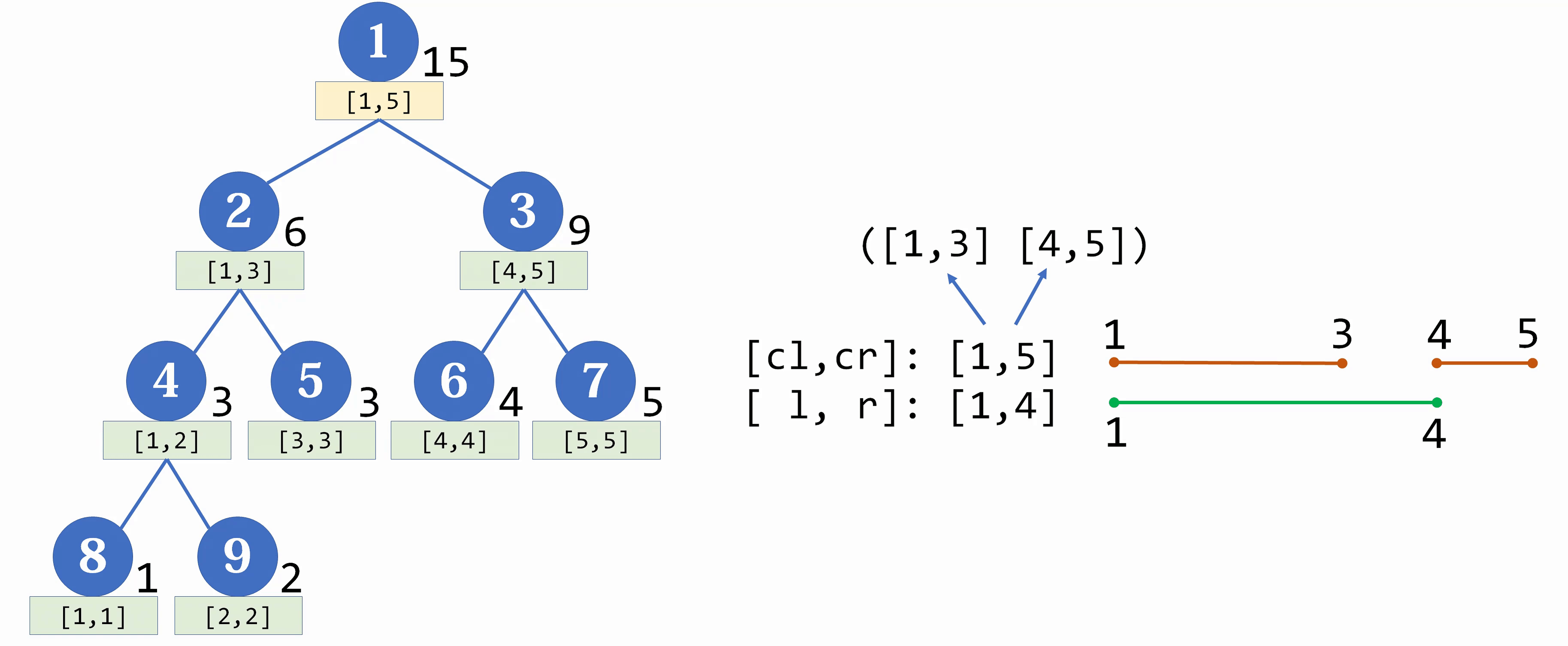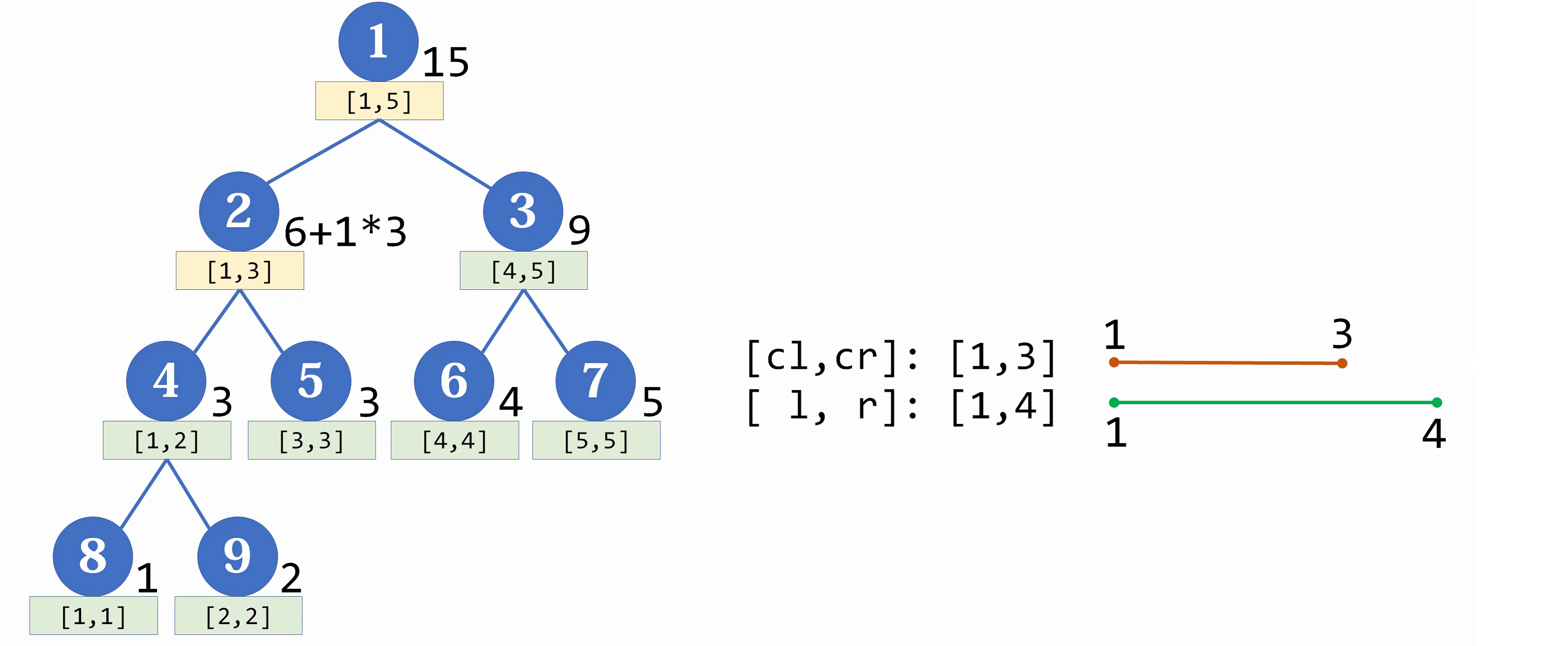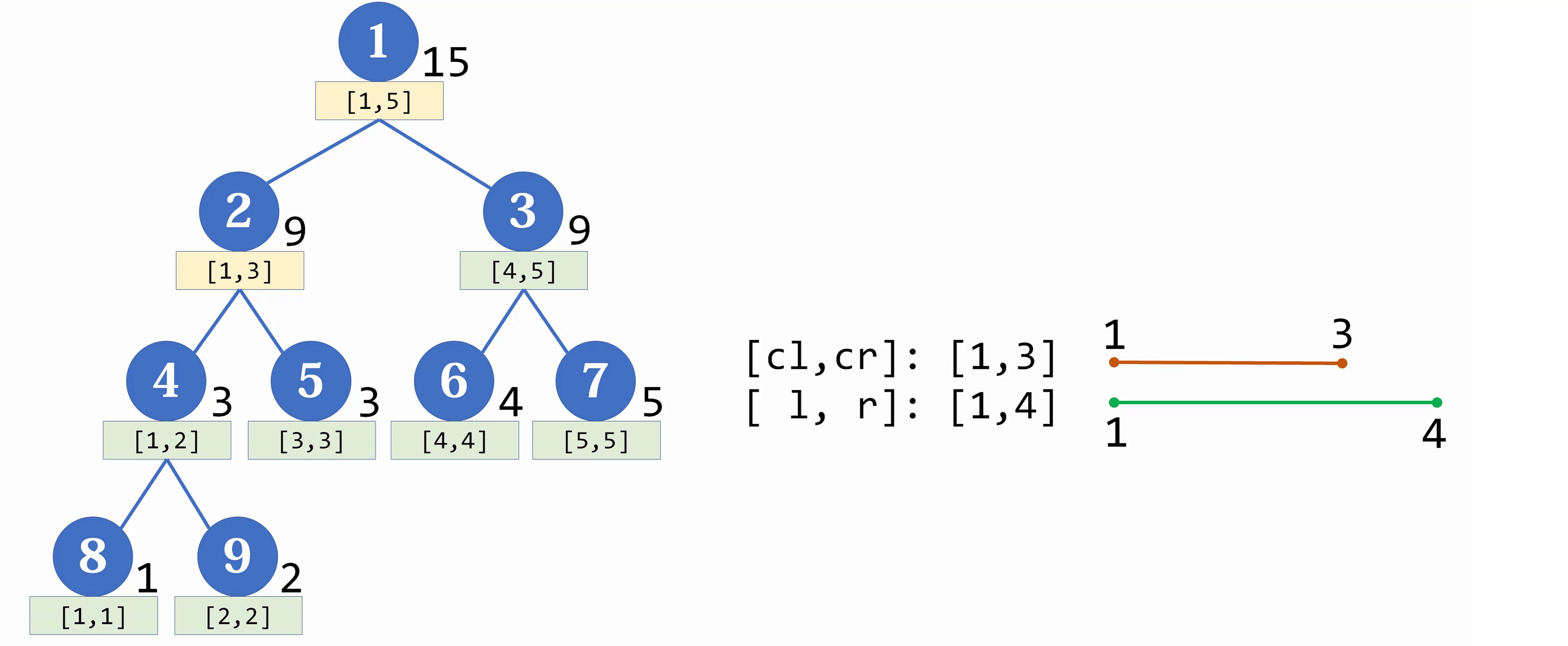
下面是一段为上面建立的线段树的区间 $[1,4]$ 加上 1 的过程:

实际上,对于上段更新部分 $18 \to 22$ 部分的代码,由于后续查询部分同样要用到,所以通常会额外封装成另一个函数 $push_down$,其代码为:
1
2
3
4
5
6
7
|
private void push_down(int p, int cLeft, int mid, int cRight){
mark[p * 2 + 1] += mark[p];
mark[p * 2 + 2] += mark[p];
tree[p * 2 + 1] += mark[p] * (mid - cLeft + 1);
tree[p * 2 + 2] += mark[p] * (cRight - mid);
mark[p] = 0;
}
|
线段树的查询
有了线段树的修改部分的经验,我们同样可以利用懒标记很快地写出查询部分的代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
public int query(int left, int right){
return query(left, right, 0, 0, n - 1);
}
private int query(int left, int right, int p, int cLeft, int cRight){
// 查询区间不包含线段树区间
if(left > cRight || right < cLeft){
return 0;
}else if(cLeft >= left && cRight <= right){ // 查询区间恰好覆盖线段树区间
return tree[p];
}else{ // 查询区间与线段树区间存在重叠,则二分查询,同时记得跟新懒标记
int mid = cLeft + (cRight - cLeft >>> 1);
push_down(p, cLeft, mid, cRight);
return query(left, right, p * 2 + 1, cLeft, mid) + query(left, right, p * 2 + 2, mid + 1, cRight);
}
}
|
结语
本文仅介绍了最基本的线段树用法,其实线段树的题目千奇百怪,而且技巧极多。在维护不同的信息时,需要注意是否需要乘区间长度、不同的标记之间是否相互影响等。下面附上用于区间和的线段树模板:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
|
class SegmentTree {
private final int[] tree;
private final int[] mark;
private final int n;
public SegmentTree(int[] nums){
n = nums.length;
tree = new int[n << 2];
Arrays.fill(tree, Integer.MIN_VALUE);
build(nums, 0, nums.length - 1, 0);
mark = new int[n << 2];
}
private void build(int[] nums, int left, int right, int p){
if(left == right){
tree[p] = nums[left];
}else{
int mid = (left + right) / 2;
build(nums, left, mid, p * 2 + 1);
build(nums, mid + 1, right, p * 2 + 2);
tree[p] = tree[p * 2 + 1] + tree[p * 2 + 2];
}
}
public void update(int left, int right, int d){
update(left, right, d, 0, 0, n - 1);
}
private void update(int left, int right, int d, int p, int cLeft, int cRight){
if(cLeft > right || cRight < left){
return;
}else if(cLeft >= left && cRight <= right){
tree[p] += (cRight - cLeft + 1) * d;
if(cLeft < cRight){
mark[p] += 1;
}
}else{
int mid = cLeft + (cRight - cLeft >>> 1);
push_down(p, cLeft, mid, cRight);
update(left, right, d, p * 2 + 1, cLeft, mid);
update(left, right, d, p * 2 + 2, mid + 1, cRight);
tree[p] = tree[p * 2 + 1] + tree[p * 2 + 2];
}
}
public int query(int left, int right){
return query(left, right, 0, 0, n - 1);
}
private int query(int left, int right, int p, int cLeft, int cRight){
if(left > cRight || right < cLeft){
return 0;
}else if(cLeft >= left && cRight <= right){
return tree[p];
}else{
int mid = cLeft + (cRight - cLeft >>> 1);
push_down(p, cLeft, mid, cRight);
return query(left, right, p * 2 + 1, cLeft, mid) + query(left, right, p * 2 + 2, mid + 1, cRight);
}
}
private void push_down(int p, int cLeft, int mid, int cRight){
mark[p * 2 + 1] += mark[p];
mark[p * 2 + 2] += mark[p];
tree[p * 2 + 1] += mark[p] * (mid - cLeft + 1);
tree[p * 2 + 2] += mark[p] * (cRight - mid);
mark[p] = 0;
}
}
|
实际上线段树还可以维护区间最值、区间 $gcd$ 等等,操作除了区间加也可以是区间乘、区间赋值,了解原理后很容易改。